Lecture 7 - Trip Assignment
CIVE 461/861: Urban Transportation Planning
Outline
- Problem definition & assumptions
- Shortest path algorithms
- Representing congestion
- Treatment of time
- Random effects
- Wardrop’s rules: System optimal & User equilibrium
- Assignment procedures: All-or-nothing, Capacity restraint, & Deterministic user equilibrium
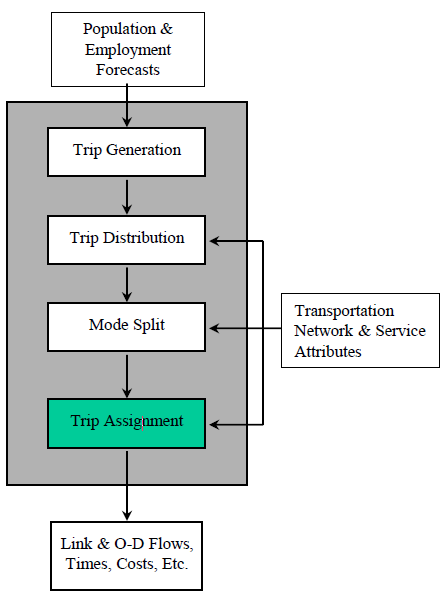
Trip Assignment Problem
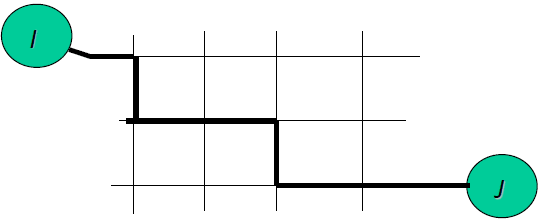
- Find the path (or paths) through the network mostly likely taken from node i to node j
- Transport network is represented by links L
- Each link has a start & end node, as well as a cost C
- Links can also be mode-specific (e.g., bus-only, bus & vehicles)
- Link cost is a function of attributes: distance, free-flow speed, capacity, & speed-flow relationship (volume-delay function)
Trip Assignment
Primary Purpose - Aggregate network performance measures
- Highway flows, transit revenues, etc.
- Zone-to-zone travel cost/time matrices
- Determine approximate link flows & identify heavily congested links
Secondary Purpose
- Determine routes between each O-D pair
- Analyze O-D pairs that use route/link
- Reasonable indication of turning movement at intersections
Trip Assignment - Basic Inputs
- Trip matrix expressing estimated demands: peak hour, 24-hour, etc.
- Person-trips need to be converted into vehicle-trips & vehicles may need to be converted into passenger car units (PCUs)
- Network as links & their properties, including speed-flow curves
- Principles or route selection rules that are relevant to problem under investigation -> choosing best route is subjective
Trip Assignment - Route Choice Issues
Differences in individual perceptions of what constitutes the best route: minimizing time, minimizing fuel consumption, or a combination of both?
Solution: Multiple user classes & generalized costs
Knowledge about alternatives varies -> apparently irrational route choices
Solution: Stochastic specifications
Congestion effects affect shorter routes first & make generalized costs comparable to initially less attractive routes
Solution: Congested assignment & equilibrium
Trip Assignment - Basic Steps
- Identify set of routes (shortest paths) that might be considered attractive to drivers between each O-D pair using shortest path algorithms
- Assign suitable proportions of trip matrix to each route -> flows on links in network
- Search for convergence
- Many techniques follow an iterative pattern of successive approximations to an ideal solution – i.e., convergence criteria
Shortest Path Calculations
- All assignment procedures depend on efficient calculation of shortest paths through large networks
- Best algorithm depends on network size & problem application (e.g., different procedures often used for road vs. transit assignment)
Shortest Path - Dijkstra Algorithm
- Find shortest path between nodes in a graph – e.g., road network
- Conceived by computer scientist Edger W. Dijkstra in 1956
- \(N\) is the set of all nodes (combination of labelled & unlabeled nodes)
- \(\hat{𝑀}\) is the set of all labelled nodes
- \(M\) is the set of un-labeled nodes
- \(n_i\) is the ith node
- \(c(n_i, n_j)\) is the cost (travel time, distance, etc.) of traveling on the link from \(n_i\) to \(n_j\)
- \(C(n_j)\) is the total cost between “initial” node & node \(n_j\)
Shortest Path - Dijkstra Algorithm 1
- Assign to every node a tentative distance value: set it to zero for the initial node & to infinity for all other nodes.
- Set the initial node as the current node & mark all other nodes as unvisited.
- For the current node, consider all its unvisited neighbors & calculate their tentative costs.
- Compare the newly calculated tentative cost to the current assigned cost & assign smaller of the two.
- E.g., if current node A is marked with a cost of 6 & the link connecting it with a neighbor node B has cost 2, then the cost to B (through A) is 6 + 2 = 8.
- If B was previously marked with a distance > 8 then change it to 8. Else, keep the current value.
Shortest Path - Dijkstra Algorithm 1
- If all neighbors of current node have been considered, then mark current node as visited & remove from unvisited set.
- If destination node has been marked visited (when planning route between two nodes) or if smallest tentative cost among nodes in unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between initial node & remaining unvisited nodes) then stop. Algorithm complete.
- Else select unvisited node marked with smallest tentative distance, set as new current node, & go to step 3.
Shortest Path - Dijkstra Algorithm 2
- Set \(k = 1\). Choose a node as the initial node. Label this node [-,0] where the minus sign indicates there is no predecessor node & the zero indicates there is zero cost associated with reaching this node. Set M equal to {\(n_1\)} where \(n_1\) is equal to the node number for the initial node.
- Set \(k = 2\). Find an unlabeled node \(n_2\) such that \(c(n_1, n_2)\) is a minimum. Assign \(n_2\) the label \([n_1, c(n_1, n_2)]\), meaning \(n_1\) is the predecessor node to \(n_2\). Add \(n_2\) to the set of labeled nodes (i.e., \(M\) now equals \(\{n_1, n_2\}\))
- Set \(k = k + 1\)
Shortest Path - Dijkstra Algorithm 2
- Find an unlabeled node \(n_k\) such that \(C(n_k) = min \{C(n_x) + min[(n_x, n_y)]\}\) for \(n_x \in M\) & \(n_y \in M’ = C(n_1) + c(n_i, n_k)\) for some \(n_i \in M\), \(n_k \in M’\). Assign the label \([n_i, C(n_k)]\) & add \(n_k\) to \(M\).
- The equation above searches over the currently labeled nodes – all nodes connected to initial node with links to unlabeled nodes. Seeks new node to connect to initial node (i.e., add to labeled set), such that path to new node has lowest travel cost from initial node.
- If all nodes labeled. Stop. Else, go to step 3.
Final product is shortest path tree rooted at node \(n_1\)
Shortest Path Example
What is the shortest path from Node 6 to All Others?

Shortest Path Example
Step 1: Cost Table
| Node pair | Cost |
|---|---|
| 6,1 | Infinity |
| 6,2 | Infinity |
| 6,3 | Infinity |
| 6,4 | Infinity |
| 6,5 | Infinity |
| 6 | 0 |
Step 2: Visitation Table
| Node | Visited? |
|---|---|
| 1 | No |
| 2 | No |
| 3 | No |
| 4 | No |
| 5 | No |
| 6 | Current |
Shortest Path Example
Step 3: Find neighbors of current node Node 6 neigbors: {1,4,5}
Step 4: Update tentative costs
| Node pair | Cost (previous cost) |
|---|---|
| 6,1 | 5 (infinity) |
| 6,4 | 3 (infinity) |
| 6,5 | 8 (infinity) |
Costs are less than previous, so update table
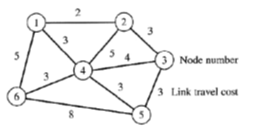
Shortest Path Example

Trip Assignment Assumptions
- Fixed costs (no congestion) vs. variable costs (congestion effects)
- Static vs. dynamic
- Deterministic vs. stochastic
- System optimization vs. user equilibrium
Fixed Cost Assumption
- Reasonable to ignore congestion effects in certain cases:
- Most transit assignment
- Most intercity cases
- Rural areas
- Small urban areas
- Off-peak time periods if volumes are low
Congestion Effects
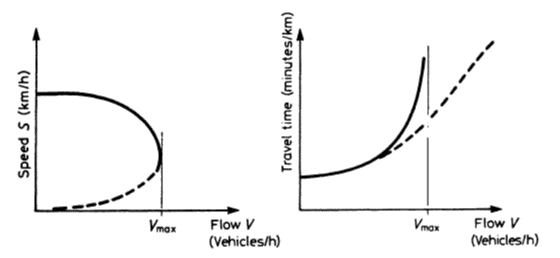
- On most urban road networks, congestion effects are significant (especially during peak periods)
- Generally, use volume-delay curve to predict link travel time (t) as function of link volume (v)
- Volume-delay functions are simple approximations to true link performance
Volume-Delay Function: Supply Curve/Performance Function

Common VDFs
- Need a continuous, differentiable function
- Bureau of Public Roads (BPR) function is most common function worldwide
- Tangent function another common method
- Converges more quickly
- More realistic results for oversaturated case
BPR Function
\[t=(\frac{L}{S})(1+a(\frac{v}{c})^b)\] \[t=t_0(1+a(\frac{v}{c})^b)\]
Where:
\(t\) = link travel time (min)
\(L\) = link length (mi)
\(S\) = link uncongested average speed (mi/min)
\(t_0\) = free-flow travel speed = L / S
\(v\) = link volume (veh/hr)
\(c\) = link capacity (veh/hr)
\(a\) = parameter = 1.0 if one-hr assignment or 0.15 if 24-hr assignment
\(b\) = parameter = 4 for arterial roads or 6 for freeway
Tangent Function
- Function identical for BPR values of v/c < 1.0 (under-saturated case)
- For v/c > 1.0 (oversaturated case), use a straight line with slope = BPR slope at v/c = 1
\[t = \begin{cases} t_0(1+a(\frac{v}{c})^b), \frac{v}{c} \leq 1 \\ t_0((1+a-ab)+ab(\frac{v}{c})), \frac{v}{c} > 1 \end{cases}\]
For \(a = 1\) & \(b = 4\), gives \(t=t_0(4(\frac{v}{c})-2)\)
Example BPR Function

Static Vs. Dynamic Assignment
- Static assignment procedures assign trips to all links on a chosen path simultaneously – i.e., time taken to travel from link to link is ignored
- Dynamic assignment procedures assign trips to each link in the chosen path sequentially, taking into account the time taken to travel along each link
- Dynamic assignment more realistic, but much more complex & computationally intensive
Deterministic Vs. Stochastic Assignment
- Deterministic assignment: Assume that travel times are known with certainty by trip-makers & they make perfectly optimal route choices
- Stochastic assignment: Travel times are not known with certainty by trip-makers &/or they are imperfect optimizers &/or include other factors in decision-making
Stochastic Assignment
- Stochastic assignment used for some applications:
- Some transit assignment algorithms
- Moderately (but not heavily) congested networks
- Highly abstracted (i.e., aggregated) networks
- Discrete route choice models (e.g., logit) exist
- Computationally burdensome
- Need to take care in defining choice set of feasible routes
Deterministic Assignment
- Deterministic assignment used in most urban applications
- Simpler & easier to use
- Computationally more efficient
- Deterministic assumptions not bad in congested networks (i.e., where penalty choosing non-optimal route is high)
Deterministic Vs. Stochastic Assignment
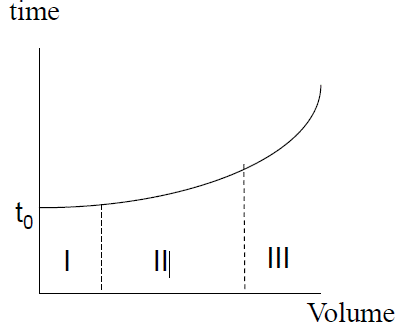
- I: in fairly uncongested condition as network is going towards saturation. Deterministic & stochastic assignment work in same way
- II: Congestion building up & deterministic approach will under-estimate effect.
- Stochastic assignment is better.
- III: Highly congested situation, small increase in volume causes larger increase in time.
- Penalty for wrong information would incur high delay. Assuming users aware of situation, deterministic assignment more appropriate.
Wardrop’s Rule
- Wardrop (1952) credited with first identifying two fundamental approaches to trip assignment
- System optimization: Assign O-D flows to paths to minimize total (average) system travel time
- User equilibrium: Assign O-D flows so no user in system can unilaterally change routes & improve his/her travel time
System Optimization
- Assign O-D flows so they generate a set of link flows {Vl} that minimizes total travel time in system \[min \sum_l V_l f(V_l)\]
- System optimization works for many freight applications or passenger travel in modes with dedicated ROW
- Does not describe human route choice well
User Equilibrium
- Each trip-maker chooses his/her route through network to minimize his/her individual travel time
- Equilibrium is achieved when every trip-maker is using best route possible, given prevailing congestion levels
- Equilibrium = no user can switch routes & improve his/her travel time, so no user will switch voluntarily
Trip Assignment Procedures for CIVE461
- All-or-nothing: Fixed cost, static, deterministic & non-equilibrium:
- Incremental assignment: Variable cost, static, deterministic & non-equilibrium procedure
- Deterministic user equilibrium (DUE): Variable cost, static, deterministic, & equilibrium assignment
All-Or-Nothing Assignment
- If no congestion effects, then DUE implies there is a single best route for each trip-maker
- Simple
- Easy to understand
- Easy to compute
- Often used for transit assignment
- Not applicable to congested road networks
All-Or-Nothing Algorithm
All-Or-Nothing Assignment: Example
OD trips to be assigned:
A-C = 400
A-D = 200
B-C = 300
B-D = 100
- Find shortest paths for A-D, A-C, B-C, & B-D
- Assign all trips to corresponding shortest paths
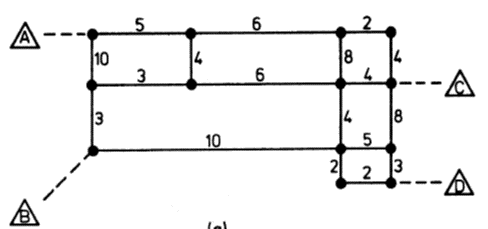
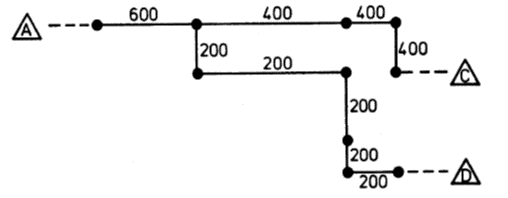
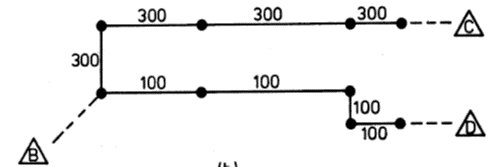
All-Or-Nothing Assignment: Example
Sum all assigned trips to get complete assignment

Incremental Assignment Methods
- Incorporating congestion into user equilibrium calculations adds significant complexity to problem
- Originally, planners used ad hoc capacity constraint methods to generate approximations to user equilibrium solution
- However, these methods generally unsatisfactory
Incremental Assignment Methods

Incremental Assignment: Example
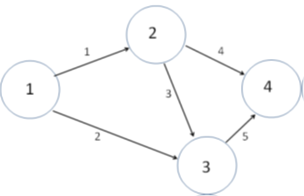
\[t_1 = \frac{t_{01}}{1-v_1/c_1}\] where:
\(t_1\) = travel time on link 1
\(t_{01}\) = travel time on link 1 under zero flow condition
\(v_1\) = volume on link 1
\(c_1\) = capacity of link 1
| Link | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(T_0\) | 10 | 15 | 3 | 5 | 4 |
| Capacity | 300 | 500 | 150 | 200 | 200 |
O-D trips to assign:
| From/To | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 100 | 100 | 100 |
| 2 | 0 | 0 | 50 | 50 |
| 3 | 0 | 0 | 0 | 100 |
| 4 | 0 | 0 | 0 | 0 |
Random assignment order:
| To | ||
|---|---|---|
| O-D Pair | 1 | 2 |
| (1,2) | 1 | 3 |
| (1,3) | 6 | 6 |
| (1,4) | 2 | 4 |
| (2,3) | 3 | 2 |
| (2,4) | 5 | 5 |
| (3,4 | 4 | 1 |
Incremental Assignment: Example
Update travel times
- 1st iteration: 50% assignment & given order
- Start with FF travel time (\(t_0\)) & update after each assignment pair
- Use updated times for next shortest path calculation
| O-D pair (1,2) : V (1,2) = 50 | |||||
|---|---|---|---|---|---|
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 50 | 0 | 0 | 0 | 0 |
| t | 12 | 15 | 3 | 5 | 4 |
| O-D pair (1,4) : V (1,4) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 0 | 0 | 50 | 0 |
| t | 15 | 15 | 3 | 6.666667 | 4 |
| O-D pair (2,3) : V (2,3) = 25 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 0 | 25 | 50 | 0 |
| t | 15 | 15 | 3.6 | 6.666667 | 4 |
| O-D pair (3,4) : V (3,4) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 0 | 25 | 50 | 50 |
| t | 15 | 15 | 3.6 | 6.666667 | 5.333333 |
| O-D pair (2,4) : V (2,4) = 25 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 0 | 25 | 75 | 50 |
| t | 15 | 15 | 3.6 | 8 | 5.333333 |
| O-D pair (1,3) : V (1,3) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 50 | 25 | 75 | 50 |
| t | 15 | 16.66667 | 3.6 | 8 | 5.333333 |
Incremental Assignment: Example
Update travel times
- 2nd iteration: 50% assignment & given order
| O-D pair (3,4) : V (3,4) = 50 | |||||
|---|---|---|---|---|---|
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 50 | 25 | 75 | 100 |
| t | 15 | 16.66667 | 3.6 | 8 | 8 |
| O-D pair (2,3) : V (2,3) = 25 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 50 | 50 | 75 | 100 |
| t | 15 | 16.66667 | 4.5 | 8 | 8 |
| O-D pair (1,2) : V (1,2) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 150 | 50 | 50 | 75 | 100 |
| t | 20 | 16.66667 | 4.5 | 8 | 8 |
| O-D pair (1,4) : V (1,4) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 150 | 100 | 50 | 75 | 150 |
| t | 20 | 18.75 | 4.5 | 8 | 16 |
| O-D pair (2,4) : V (2,4) = 25 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 150 | 100 | 50 | 100 | 150 |
| t | 20 | 18.75 | 4.5 | 10 | 16 |
| Final Flow and Corresponding Travel Time on Links | |||||
| O-D pair (1,3) : V (1,3) = 50 | |||||
| Link | 1 | 2 | 3 | 4 | 5 |
| V | 150 | 150 | 50 | 100 | 150 |
| t | 20 | 21.42857 | 4.5 | 10 | 16 |
Capacity Constrained Deterministic User Equilibrium (DUE)
- Note the two routes between same O-D pair will be used by trip-makers iff the travel times on the two routes are the same.
- Consider a single O-D pair (origin A & destination B) with two links (routes) connection them (1 & 2)

DUE Assignment: Example
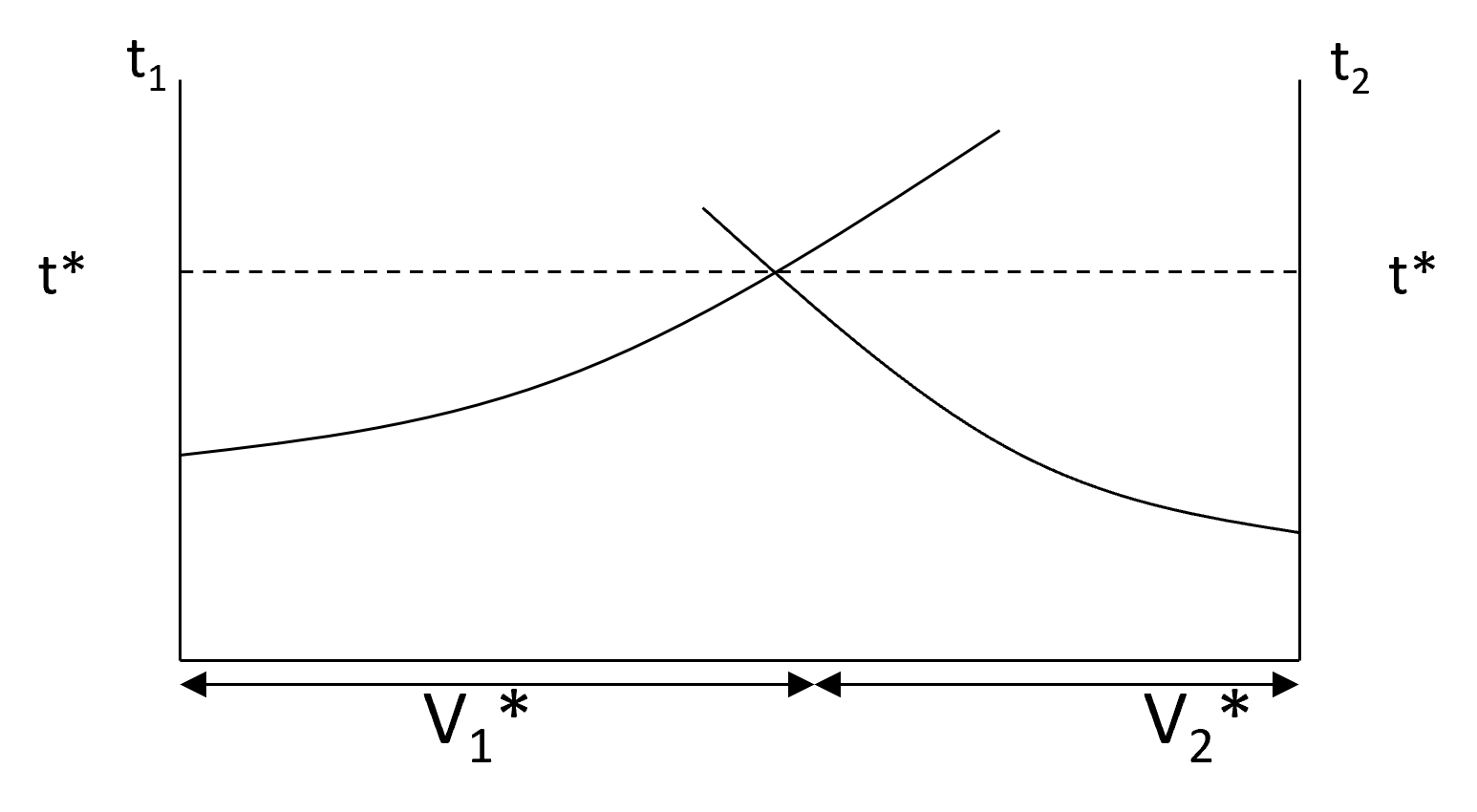
Must determine link flows {V1, V2} such that \[𝑉_1+𝑉_2=𝑉_𝐴𝐵\] \[𝑡_1=𝑡_2=𝑡^∗\] Where \(t^*\) is the equilibrium travel time between A & B
Volume-Delay Functions (VDF) for Links 1 & 2

Equilibrium Solution
\[𝐹_1=\int_0^{𝑣_1^∗} f_1(v_1) dv_1 \] \[𝐹_2=\int_0^{v_2^*}f_2(v_2) dv_2 \]
- At equilibrium, minimum \(F = F1 + F2\)
- At any non-equilibrium point, total area under both curves is not minimum: there is extra shaded area
Equilibrium Solution
- Special case: curves may not intersect
- Here, optimum is area under \(f_2(v_2)\)
![]()
Frank-Wolfe Algorithm
- Equilibrium link volumes are such that the sum of the areas under the volume-delay curves equals the minimum value achievable:
- F(V) given by \[min \sum_l \int_0^{v_l}f_l(v) d(v) \text{ (𝐸𝑄1)}\]
- Above equation generalizes to any number of O-D pairs & any number of links per path
Frank-Wolfe Algorithm

Frank-Wolfe Algorithm

Three Route Example
flowchart LR A[P] ---->|1| B(Q) A[P] ---->|2| B(Q) A[P] ---->|3| B(Q)
\[f_1(v_1) = 10(1+0.15(v_1/200)^4)\] \[f_2(v_2) = 20(1+0.15(v_1/400)^4)\] \[f_3(v_3) = 25(1+0.15(v_1/300)^4)\]
Three Route Example - Solution
We’ll start by creating a Pandas dataframe to store the iteration variables
import pandas as pd
import numpy as np
from scipy.optimize import minimize_scalar
df = pd.DataFrame({"f1": pd.Series(dtype='float'),
"f2": pd.Series(dtype='float'),
"f3": pd.Series(dtype='float'),
"V1": pd.Series(dtype='float'),
"V2": pd.Series(dtype='float'),
"V3": pd.Series(dtype='float'),
"F1": pd.Series(dtype='float'),
"F2": pd.Series(dtype='float'),
"F3": pd.Series(dtype='float'),
"F": pd.Series(dtype='float'),
"lambda": pd.Series(dtype='float')})Three Route Example - Solution
We can then define the inputs to the traffic assignment algorithm.
# Specify the freeflow travel times/capacities
ff_tt_1 = 10
ff_tt_2 = 20
ff_tt_3 = 25
C1 = 200
C2 = 400
C3 = 300
volume = 1000 # veh/hr
min_tt = np.min([ff_tt_1, ff_tt_2, ff_tt_3]) # minimum travel time
# Define the volumes on each link (1,2, and 3)
V1 = volume if (ff_tt_1==min_tt) else 0
V2 = volume if (ff_tt_2==min_tt) else 0
V3 = volume if (ff_tt_3==min_tt) else 0
# Define total costs as integrals of travel time costs over volume
F1 = ff_tt_1*V1 + ff_tt_1*0.15/C1**4*V1**5/5
F2 = ff_tt_2*V2 + ff_tt_2*0.15/C2**4*V2**5/5
F3 = ff_tt_3*V3 + ff_tt_3*0.15/C3**4*V3**5/5
F = F1 + F2 + F3
l = 1.0 # intialize lambda to 1.0
tol = 10**-2 # tolerance on the difference in total cost between iterations
row = [ff_tt_1, ff_tt_2, ff_tt_3, V1, V2, V3, F1, F2, F3, F, l]
df.loc[len(df),:] = row # add initial values to dfThree Route Example - Solution
Next we define the Frank-Wolfe algorithm and solve for \(\lambda\) using scipy optimize minimize_scalar. The first step is to define a loop that repeatedly calls the minimization on a new set of volumes. We define the Frank-Wolfe algorithm and solve for \(\lambda\) using scipy optimize minimize_scalar. The next step is to define the optimization problem. We’ll define the optimization in two functions: get_optimal_vals calculates the various values we need in each iteration and FW_Alg defines the function to be minized by scipy optimize minimize_scalar.
# Apply the Frank-Wolfe algorithm on the example dataset
def FW_Alg(x, prev_iter):
f1, f2, f3, V1, V2, V3, F1, F2, F3 = get_optimal_vals(x, prev_iter)
return (F1 + F2 + F3)
# Function computes the various traffic assignment algorithm values at optimality
def get_optimal_vals(x, prev_iter):
f1 = ff_tt_1*(1+0.15*(prev_iter["V1"]/C1)**4)
f2 = ff_tt_2*(1+0.15*(prev_iter["V2"]/C2)**4)
f3 = ff_tt_3*(1+0.15*(prev_iter["V3"]/C3)**4)
min_tt = np.min([f1, f2, f3]) # minimum travel time
V1 = x*prev_iter["V1"] + (1-x)*(volume if f1==min_tt else 0)
V2 = x*prev_iter["V2"] + (1-x)*(volume if f2==min_tt else 0)
V3 = x*prev_iter["V3"] + (1-x)*(volume if f3==min_tt else 0)
F1 = ff_tt_1*V1 + ff_tt_1*0.15/C1**4*V1**5/5
F2 = ff_tt_2*V2 + ff_tt_2*0.15/C2**4*V2**5/5
F3 = ff_tt_3*V3 + ff_tt_3*0.15/C3**4*V3**5/5
return f1, f2, f3, V1, V2, V3, F1, F2, F3
F_diff = F
while F_diff > tol:
F_diff = F
prev_iter = df.iloc[-1] # Get the values from the last iteration
res = minimize_scalar(FW_Alg, args=(prev_iter), bounds=[0,1])
F = res.fun
l = res.x
f1, f2, f3, V1, V2, V3, F1, F2, F3 = get_optimal_vals(l, prev_iter)
row = [f1, f2, f3, V1, V2, V3, F1, F2, F3, F, l]
df.loc[len(df),:] = row
F_diff = F_diff - FThree Route Example - Solution
Putting everything together, we can print a table summarizing the variable values at each iteration.
| f1 | f2 | f3 | V1 | V2 | V3 | F1 | F2 | F3 | F | lambda | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10.00 | 20.00 | 25.00 | 1000.00 | 0.00 | 0.00 | 197500.00 | 0.00 | 0.00 | 197500.00 | 1.00 |
| 1 | 947.50 | 20.00 | 25.00 | 403.46 | 596.54 | 0.00 | 6039.00 | 13701.45 | 0.00 | 19740.44 | 0.40 |
| 2 | 34.84 | 34.84 | 25.00 | 338.45 | 500.42 | 161.13 | 4217.09 | 10743.87 | 4038.43 | 18999.39 | 0.84 |
| 3 | 22.30 | 27.35 | 25.31 | 361.97 | 482.63 | 155.41 | 4784.70 | 10266.28 | 3893.55 | 18944.53 | 0.96 |
| 4 | 26.09 | 26.36 | 25.27 | 354.58 | 472.78 | 172.64 | 4596.77 | 10009.25 | 4330.12 | 18936.14 | 0.98 |
| 5 | 24.82 | 25.85 | 25.41 | 359.22 | 469.38 | 171.40 | 4713.80 | 9921.62 | 4298.58 | 18934.00 | 0.99 |
| 6 | 25.61 | 25.69 | 25.40 | 357.30 | 466.87 | 175.83 | 4664.85 | 9857.20 | 4411.38 | 18933.43 | 0.99 |
| 7 | 25.28 | 25.57 | 25.44 | 358.58 | 465.93 | 175.48 | 4697.45 | 9833.37 | 4402.44 | 18933.27 | 1.00 |
Transit Assignment
- Transit assignment not usually a function of congestion
- Procedures typically used:
- All-Or-Nothing
- Stochastic (multipath)
- Must account for:
- Walk access/egress times
- Waiting times as f(headway)
- Transfers
- Feasible transfer points
- Transfer times

